Electron Hole
From: https://en.wikipedia.org/wiki/Electron_hole 



Electron hole


In physics, chemistry, and electronic engineering, an electron hole (often
simply called a hole) is a quasiparticle denoting the lack of an electron at
a position where one could exist in an atom or atomic lattice. Since in a
normal atom or crystal lattice the negative charge of the electrons is
balanced by the positive charge of the atomic nuclei, the absence of an
electron leaves a net positive charge at the hole's location.

Holes in a metal[1] or semiconductor crystal lattice can move through the
lattice as electrons can, and act similarly to positively-charged particles.
They play an important role in the operation of semiconductor devices such
as transistors, diodes (including light-emitting diodes) and integrated
circuits. If an electron is excited into a higher state it leaves a hole in
its old state. This meaning is used in Auger electron spectroscopy (and
other x-ray techniques), in computational chemistry, and to explain the low
electron-electron scattering-rate in crystals (metals and semiconductors).
Although they act like elementary particles, holes are rather
quasiparticles; they are different from the positron, which is the
antiparticle of the electron. (See also Dirac sea.)

	
	


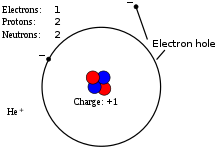
When an electron leaves a helium atom, it leaves an electron hole in its place. This causes the helium atom to become positively charged.



In crystals, electronic band structure calculations lead to an effective mass
for the electrons that is typically negative at the top of a band. The negative
mass is an unintuitive concept,[2] and in these situations, a more familiar 
picture is found by considering a positive charge with a positive mass.




Solid-state physics

In solid-state physics, an electron hole (usually referred to simply as a
hole) is the absence of an electron from a full valence band. A hole is
essentially a way to conceptualize the interactions of the electrons within
a nearly full valence band of a crystal lattice, which is missing a small
fraction of its electrons. In some ways, the behavior of a hole within a
semiconductor crystal lattice is comparable to that of the bubble in a full
bottle of water.[3]

The hole concept was pioneered in 1929 by Rudolf Peierls, who analyzed the
Hall effect using Bloch's theorem, and demostrated that a nearly full and a
nearly empty Brillouin zones give the opposite Hall voltages. The concept of
an electron hole in solid-state physics predates the concept of a hole in
Dirac equation, but there is no evidence that it would have influenced
Dirac's thinking.[4]




Simplified analogy: Empty seat in an auditorium 


A children's puzzle which illustrates the mobility of holes in an atomic
lattice. The tiles are analogous to electrons, while the missing tile (lower
right corner) is analogous to a hole. Just as the position of the missing
tile can be moved to different locations by moving the tiles, a hole in a
crystal lattice can move to different positions in the lattice by the motion
of the surrounding electrons.

Hole conduction in a valence band can be explained by the following
analogy:

Imagine a row of people seated in an auditorium, where there are no spare
chairs. Someone in the middle of the row wants to leave, so he jumps over
the back of the seat into another row, and walks out. The empty row is
analogous to the conduction band, and the person walking out is analogous to
a conduction electron.

Now imagine someone else comes along and wants to sit down. The empty row
has a poor view; so he does not want to sit there. Instead, a person in the
crowded row moves into the empty seat the first person left behind. The
empty seat moves one spot closer to the edge and the person waiting to sit
down. The next person follows, and the next, et cetera. One could say that
the empty seat moves towards the edge of the row. Once the empty seat
reaches the edge, the new person can sit down.

In the process everyone in the row has moved along. If those people were
negatively charged (like electrons), this movement would constitute
conduction. If the seats themselves were positively charged, then only the
vacant seat would be positive. This is a very simple model of how hole
conduction works.

Instead of analyzing the movement of an empty state in the valence band as
the movement of many separate electrons, a single equivalent imaginary
particle called a "hole" is considered. In an applied electric field, the
electrons move in one direction, corresponding to the hole moving in the
other. If a hole associates itself with a neutral atom, that atom loses an
electron and becomes positive. Therefore, the hole is taken to have positive
charge of +e, precisely the opposite of the electron charge.

	
	 

A children's puzzle which 
illustrates the mobility of holes in 
an atomic lattice. The tiles are 
analogous to electrons, while the 
missing tile (lower right corner) is 
analogous to a hole. Just as the 
position of the missing tile can be 
moved to different locations by 
moving the tiles, a hole in a 
crystal lattice can move to 
different positions in the lattice by 
the motion of the surrounding 
electrons.



In reality, due to the uncertainty principle of quantum mechanics, combined with
the energy levels available in the crystal, the hole is not localizable to a
single position as described in the previous example. Rather, the positive 
charge which represents the hole spans an area in the crystal lattice covering
many hundreds of unit cells. This is equivalent to being unable to tell which 
broken bond corresponds to the "missing" electron. Conduction band electrons are
similarly delocalized.




Detailed picture: A hole is the
absence of a negative-mass electron


The analogy above is quite simplified, and cannot explain why holes create an
opposite effect to electrons in the Hall effect and Seebeck effect. A more 
precise and detailed explanation follows.[5]

 	The dispersion relation determines how electrons respond to forces (via the
concept of effective mass).[5]

A dispersion relation is the relationship between wavevector (k-vector) and
energy in a band, part of the electronic band structure. In quantum
mechanics, the electrons are waves, and energy is the wave frequency. A
localized electron is a wavepacket, and the motion of an electron is given
by the formula for the group velocity of a wave. An electric field affects
an electron by gradually shifting all the wavevectors in the wavepacket, and
the electron accelerates when its wave group velocity changes. Therefore,
again, the way an electron responds to forces is entirely determined by its
dispersion relation. An electron floating in space has the dispersion
relation E = ℏ2k2/(2m), where m is the (real) electron mass and ℏ is
reduced Planck constant. Near the bottom of the conduction band of a
semiconductor, the dispersion relation is instead E = ℏ2k2/(2m*) (m* is
the effective mass), so a conduction-band electron responds to forces as if
it had the mass m*.

	
	 


A semiconductor electronic band structure (right) includes the dispersion
relation of each band, i.e. the energy of an electron E as a function of the
electron's wavevector k. The "unfilled band" is the semiconductor's conduction band; it
curves upward indicating positive effective mass. The "filled band" is the
semiconductor's valence band; it curves downward indicating negative
effective mass.



Electrons near the top of the valence band behave as if they have negative
mass.[5]

The dispersion relation near the top of the valence band is E = ℏ2k2/(2m*)
with negative effective mass. So electrons near the top of the valence band
behave like they have negative mass. When a force pulls the electrons to the
right, these electrons actually move left. This is solely due to the shape
of the valence band and is unrelated to whether the band is full or empty.
If you could somehow empty out the valence band and just put one electron
near the valence band maximum (an unstable situation), this electron would
move the "wrong way" in response to forces.
Positively-charged holes as a shortcut for calculating the total current of
an almost-full band.[5]

A perfectly full band always has zero current. One way to think about this
fact is that the electron states near the top of the band have negative
effective mass, and those near the bottom of the band have positive
effective mass, so the net motion is exactly zero. If an otherwise-almost
-full valence band has a state without an electron in it, we say that this
state is occupied by a hole. There is a mathematical shortcut for
calculating the current due to every electron in the whole valence band:
Start with zero current (the total if the band were full), and subtract the
current due to the electrons that would be in each hole state if it wasn't a
hole. Since subtracting the current caused by a negative charge in motion is
the same as adding the current caused by a positive charge moving on the
same path, the mathematical shortcut is to pretend that each hole state is
carrying a positive charge, while ignoring every other electron state in the
valence band.
A hole near the top of the valence band moves the same way as an electron
near the top of the valence band would move[5] (which is in the opposite
direction compared to conduction-band electrons experiencing the same
force.)

This fact follows from the discussion and definition above. This is an
example where the auditorium analogy above is misleading. When a person
moves left in a full auditorium, an empty seat moves right. But in this
section we are imagining how electrons move through k-space, not real space,
and the effect of a force is to move all the electrons through k-space in
the same direction at the same time. In this context, a better analogy is a
bubble underwater in a river: The bubble moves the same direction as the
water, not the opposite.

Since force = mass × acceleration, a negative-effective-mass electron near
the top of the valence band would move the opposite direction as a positive
-effective-mass electron near the bottom of the conduction band, in response
to a given electric or magnetic force. Therefore, a hole moves this way as
well.
Conclusion: Hole is a positive-charge, positive-mass quasiparticle.

From the above, a hole (1) carries a positive charge, and (2) responds to
electric and magnetic fields as if it had a positive charge and positive
mass. (The latter is because a particle with positive charge and positive
mass respond to electric and magnetic fields in the same way as a particle
with a negative charge and negative mass.) That explains why holes can be
treated in all situations as ordinary positively charged quasiparticles.




Role in semiconductor technology
In some semiconductors, such as silicon, the hole's effective mass is
dependent on a direction (anisotropic), however a value averaged over all
directions can be used for some macroscopic calculations.

In most semiconductors, the effective mass of a hole is much larger than
that of an electron. This results in lower mobility for holes under the
influence of an electric field and this may slow down the speed of the
electronic device made of that semiconductor. This is one major reason for
adopting electrons as the primary charge carriers, whenever possible in
semiconductor devices, rather than holes. This is also why NMOS logic is
faster than PMOS logic. OLED screens have been modified to reduce imbalance
resulting in non radiative recombination by adding extra layers and/or
decreasing electron density on one plastic layer so electrons and holes
precisely balance within the emission zone. However, in many semiconductor
devices, both electrons and holes play an essential role. Examples include
p–n diodes, bipolar transistors, and CMOS logic.




Holes in quantum chemistry
An alternate meaning for the term electron hole is used in computational
chemistry. In coupled cluster methods, the ground (or lowest energy) state of a
molecule is interpreted as the "vacuum state"—conceptually, in this state, there
are no electrons. In this scheme, the absence of an electron from a normally
filled state is called a "hole" and is treated as a particle, and the presence
of an electron in a normally empty state is simply called an "electron". This
terminology is almost identical to that used in solid-state physics.




See also





Particles in Physics




v.t.e







Particles in physics



Elementary	
Fermions	
Quarks	

 Up (quark antiquark) Down (quark antiquark) Charm (quark antiquark) Strange
(quark antiquark) Top (quark antiquark) Bottom (quark antiquark)



Leptons	
 Electron Positron Muon Antimuon Tau Antitau Neutrino
 Electron neutrino Electron antineutrino Muon neutrino Muon antineutrino Tau
neutrino Tau antineutrino



Bosons	
Gauge	
Photon Gluon W and Z bosons



Scalar	
Higgs boson 



Ghost fields	
Faddeev–Popov ghosts



Hypothetical	
Superpartners	
Gauginos	
Gluino Gravitino Photino



Others	
Axino Chargino Higgsino Neutralino Sfermion (Stop squark)



Others	
Axion Curvaton Dilaton Dual graviton Graviphoton Graviton Inflaton
Leptoquark Magnetic monopole Majoron Majorana fermion Dark photon Preon
Sterile neutrino Tachyon W′ and Z′ bosons X and Y bosons



Composite	
Hadrons	
Baryons	

Nucleon Proton Antiproton Neutron Antineutron Delta baryon Lambda baryon Sigma
baryon Xi baryon Omega baryon



Mesons	
Pion Rho meson Eta and eta prime mesons Bottom eta meson Phi meson J/psi
meson Omega meson Upsilon meson Kaon B meson D meson Quarkonium



Exotic hadrons	
 Tetraquark (Double-charm tetraquark) Pentaquark



Others	
Atomic nuclei Atoms Exotic atoms
 Positronium Muonium Tauonium Onia Pionium Protonium Superatoms Molecules



Hypothetical	
Baryons	
Hexaquark Heptaquark Skyrmion



Mesons	
Glueball Theta meson T meson



Others	
Mesonic molecule Pomeron Diquark R-hadron



Quasiparticles	
Anyon Davydov soliton Dropleton Exciton Fracton Hole Magnon Phonon
Plasmaron Plasmon Polariton Polaron Roton Trion



Lists	
Baryons Mesons Particles Quasiparticles Timeline of particle discoveries



Related	
 History of subatomic physics
 timeline Standard Model
 mathematical formulation Subatomic particles Particles Antiparticles
Nuclear physics Eightfold way
 Quark model Exotic matter Massless particle Relativistic particle Virtual
particle Wave–particle duality Particle chauvinism



Physics portal



Authority control databases: National
 Germany Israel United States



Categories:

 Electronics conceptsQuasiparticlesQuantum chemistryCharge carriersHoles