Review of R, X, and Z (Resistance, Reactance and Impedance)

Before we begin to explore the effects of resistors, inductors, and
capacitors connected together in the same AC circuits, let’s briefly
review some basic terms and facts.



Resistance
This is essentially friction against the flow of current. It is present in
all conductors to some extent (except superconductors!), most notably in
resistors. When the alternating current goes through a resistance, a voltage
drop is produced that is in-phase with the current. Resistance is
mathematically symbolized by the letter “R” and is measured in the unit
of ohms (Ω).



Reactance
This is essentially inertia against the flow of current. It is present
anywhere electric or magnetic fields are developed in proportion to an
applied voltage or current, respectively; but most notably in capacitors and
inductors.

When the alternating current goes through a pure reactance, a voltage drop
is produced that is 90° out of phase with the current. Reactance is
mathematically symbolized by the letter “X” and is measured in the unit
of ohms (Ω).


Impedance

This is a comprehensive expression of any and all forms of opposition to
current flow, including both resistance and reactance. It is present in all
circuits, and in all components.

When the alternating current goes through an impedance, a voltage drop is
produced that is somewhere between 0° and 90° out of phase with the
current. Impedance is mathematically symbolized by the letter “Z” and is
measured in the unit of ohms (Ω), in complex form.

Perfect resistors possess resistance, but not reactance. Perfect inductors
and perfect capacitors possess reactance but no resistance. All components
possess impedance, and because of this universal quality, it makes sense to
translate all component values (resistance, inductance, capacitance) into
common terms of impedance as the first step in analyzing an AC circuit.
	
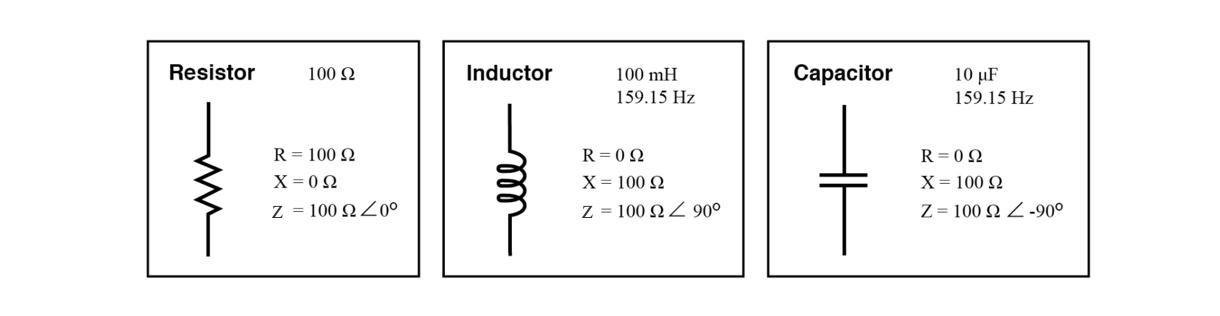	Perfect resistor, inductor, and capacitor.

The impedance phase angle for any component is the phase shift between the
voltage across that component and current through that component.

For a perfect resistor, the voltage drop and current are always in phase
with each other, and so the impedance angle of a resistor is said to be 0°.
For a perfect inductor, voltage drop always leads current by 90°, and so an
inductor’s impedance phase angle is said to be +90°.

For a perfect capacitor, voltage drop always lags current by 90°, and so a
capacitor’s impedance phase angle is said to be -90°.

Impedances in AC behave analogously to resistances in DC circuits: they add
in series, and they diminish in parallel. A revised version of Ohm’s Law,
based on impedance rather than resistance, looks like this:
	
	ohms law for ac circuits

RELATED WORKSHEETS:

    Impedance Worksheet
    AC Power Worksheet
    Capacitive Reactance Worksheet
    Inductive Reactance Worksheet