Simple Parallel (Tank Circuit) Resonance
Resonance in a Tank Circuit A condition of resonance will be experienced in a tank circuit when the reactance of the capacitor and inductor are equal to each other. Because inductive reactance increases with increasing frequency and capacitive reactance decreases with increasing frequency, there will only be one frequency where these two reactances will be equal. Example:
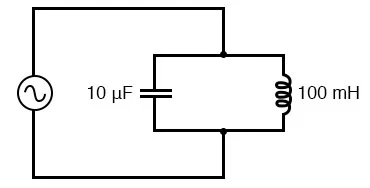Simple parallel resonant circuit (tank circuit).
In the above circuit, we have a 10 µF capacitor and a 100 mH inductor.
Since we know the equations for determining the reactance of each at a given
frequency, and we’re looking for that point where the two reactances are
equal to each other, we can set the two reactance formula equal to each
other and solve for frequency algebraically:
equations for determining the reactance
So there we have it: a formula to tell us the resonant frequency of a tank
circuit, given the values of inductance (L) in Henrys and capacitance (C) in
Farads. Plugging in the values of L and C in our example circuit, we arrive
at a resonant frequency of 159.155 Hz.
Calculating Individual Impedances What happens at resonance is quite interesting. With capacitive and inductive reactances equal to each other, the total impedance increases to infinity, meaning that the tank circuit draws no current from the AC power source! We can calculate the individual impedances of the 10 µF capacitor and the 100 mH inductor and work through the parallel impedance formula to demonstrate this mathematically:
individual impedances equation
As you might have guessed, I chose these component values to give resonance
impedances that were easy to work with (100 Ω even).
Parallel Impedance Formula Now, we use the parallel impedance formula to see what happens to total Z:
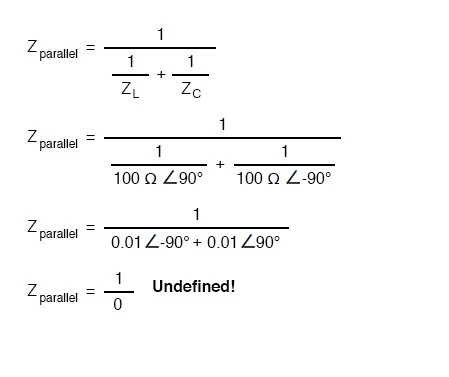parallel impedance formula to see what happens to total Z
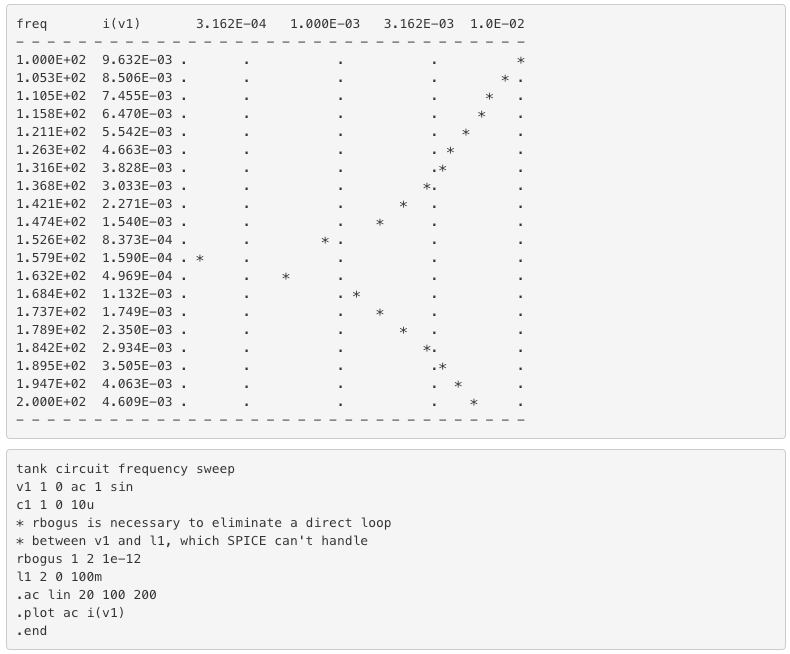
SPICE Simulation Plot We can’t divide any number by zero and arrive at a meaningful result, but we can say that the result approaches a value of infinity as the two parallel impedances get closer to each other. What this means in practical terms is that, the total impedance of a tank circuit is infinite (behaving as an open circuit) at resonance. We can plot the consequences of this over a wide power supply frequency range with a short SPICE simulation.
wide power supply frequency range with a short SPICE simulation.
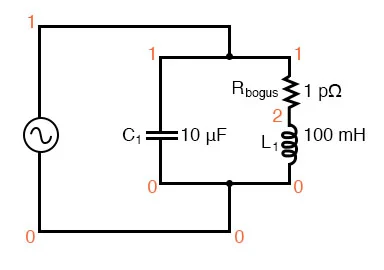
Resonant circuit suitable for SPICE simulation.
The 1 pico-ohm (1 pΩ) resistor is placed in this SPICE analysis to overcome
a limitation of SPICE: namely, that it cannot analyze a circuit containing a
direct inductor-voltage source loop. (Figure below) A very low resistance
value was chosen so as to have minimal effect on circuit behavior.
This SPICE simulation plots circuit current over a frequency range of 100 to
200 Hz in twenty even steps (100 and 200 Hz inclusive). Current magnitude on
the graph increases from left to right, while frequency increases from top
to bottom.
The current in this circuit takes a sharp dip around the analysis point of
157.9 Hz, which is the closest analysis point to our predicted resonance
frequency of 159.155 Hz. It is at this point that total current from the
power source falls to zero.
The “Nutmeg” Graphical Post-Processor Plot The plot above is produced from the above spice circuit file ( *.cir), the command (.plot) in the last line producing the text plot on any printer or terminal. A better looking plot is produced by the “nutmeg” graphical post-processor, part of the spice package. The above spice ( *.cir) does not require the plot (.plot) command, though it does no harm. The following commands produce the plot below: spice -b -r resonant.raw resonant.cir ( -b batch mode, -r raw file, input is resonant.cir) nutmeg resonant.raw From the nutmeg prompt: setplot ac1 (setplot {enter} for list of plots) >display (for list of signals) >plot mag(v1#branch) (magnitude of complex current vector v1#branch)
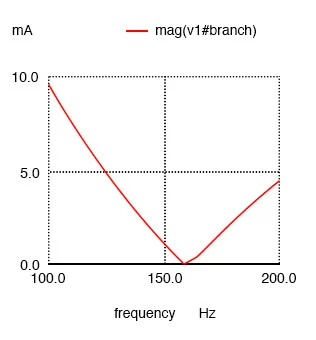Nutmeg produces plot of current I(v1) for parallel resonant circuit.
Bode Plots Incidentally, the graph output produced by this SPICE computer analysis is more generally known as a Bode plot. Such graphs plot amplitude or phase shift on one axis and frequency on the other. The steepness of a Bode plot curve characterizes a circuit’s “frequency response,” or how sensitive it is to changes in frequency.
REVIEW:
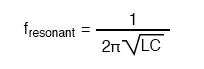For a tank circuit with no resistance (R), resonant frequency can be
calculated with the following formula