Parallel R, L, and C

We can take the same components from the series circuit and rearrange them
into a parallel configuration for an easy example circuit:
	
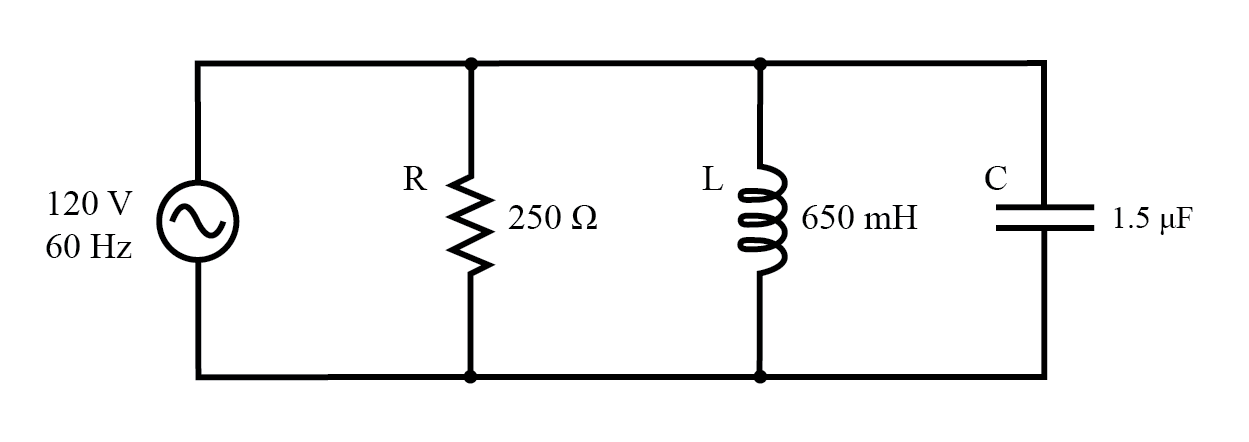
Example R, L, and C parallel circuit.
 


Impedance in Parallel Components
The fact that these components are connected in parallel instead of series
now has absolutely no effect on their individual impedances. So long as the
power supply is the same frequency as before, the inductive and capacitive
reactances will not have changed at all.

	
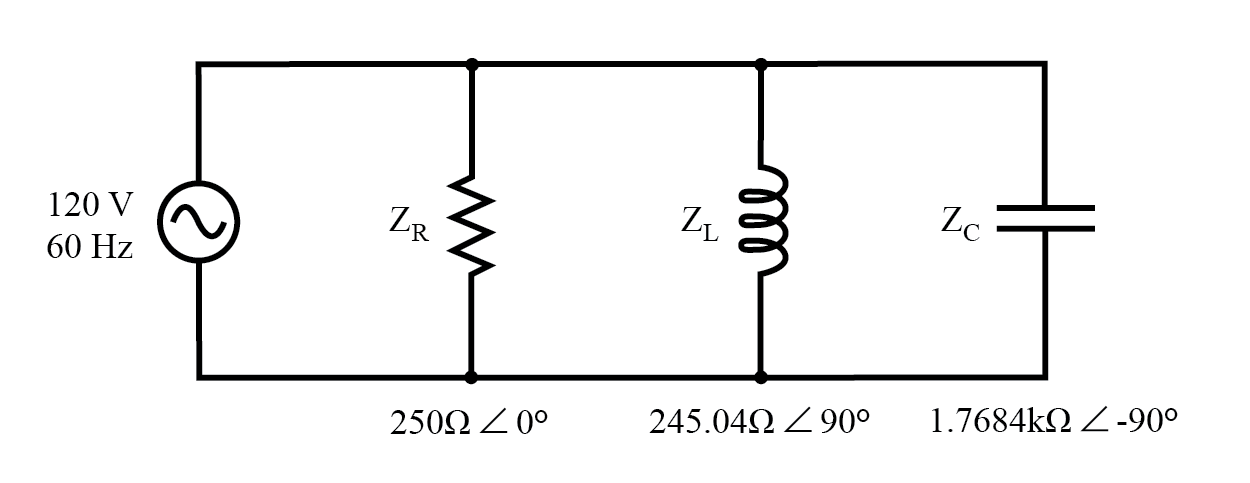	Example R, L, and C parallel circuit with impedances replacing component
values.

With all component values expressed as impedances (Z), we can set up an
analysis table and proceed as in the last example problem, except this time
following the rules of parallel circuits instead of series:
	
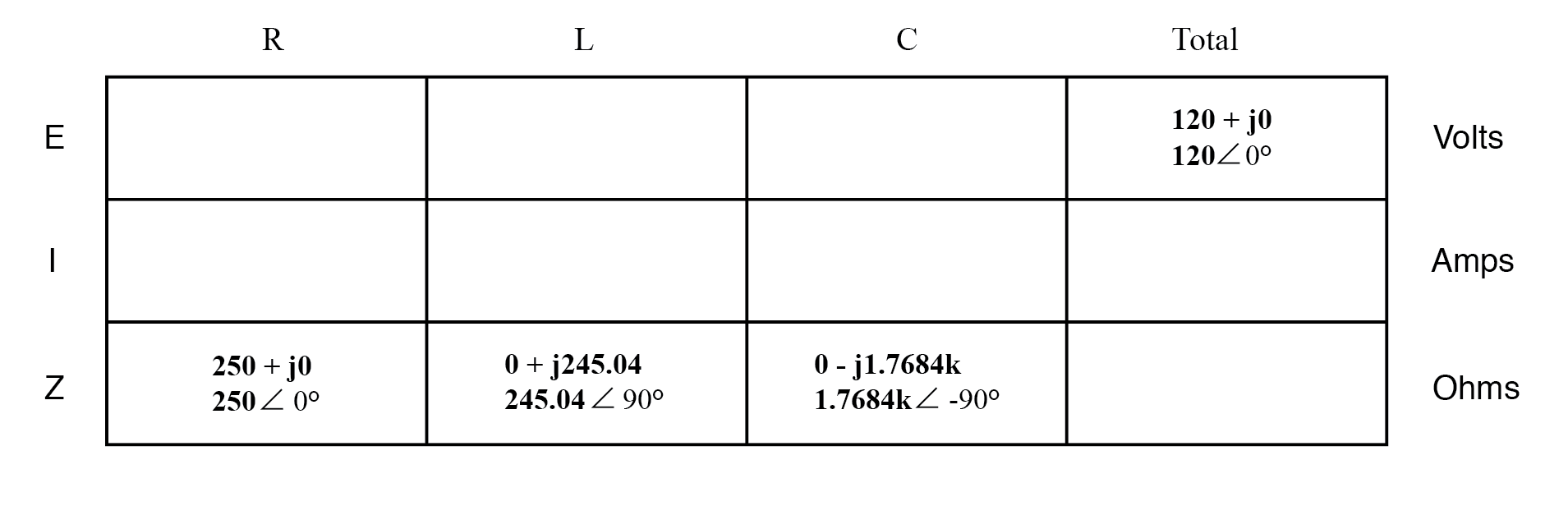	components values express as impedance image 1

Knowing that voltage is shared equally by all components in a parallel
circuit, we can transfer the figure for total voltage to all component
columns in the table:

	
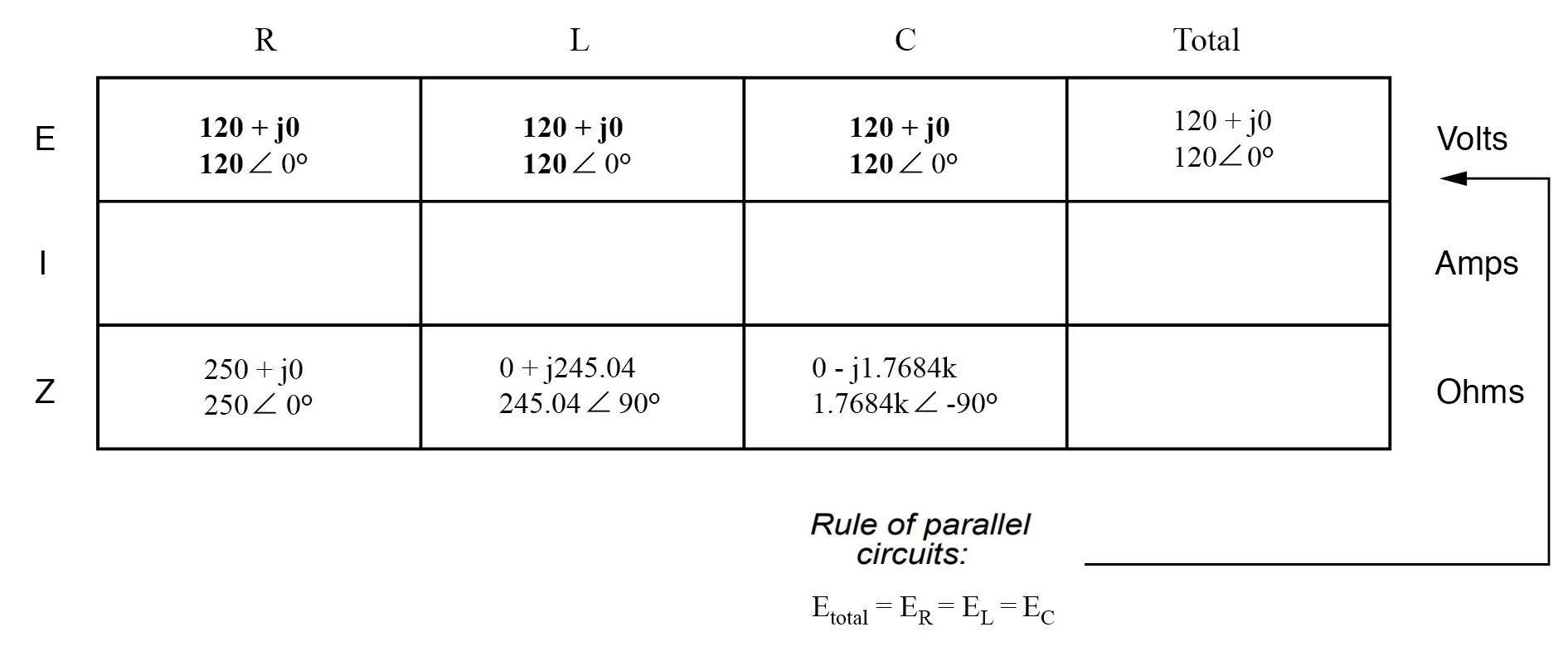	components values express as impedance image 2

Now, we can apply Ohm’s Law (I=E/Z) vertically in each column to determine
the current through each component:
	
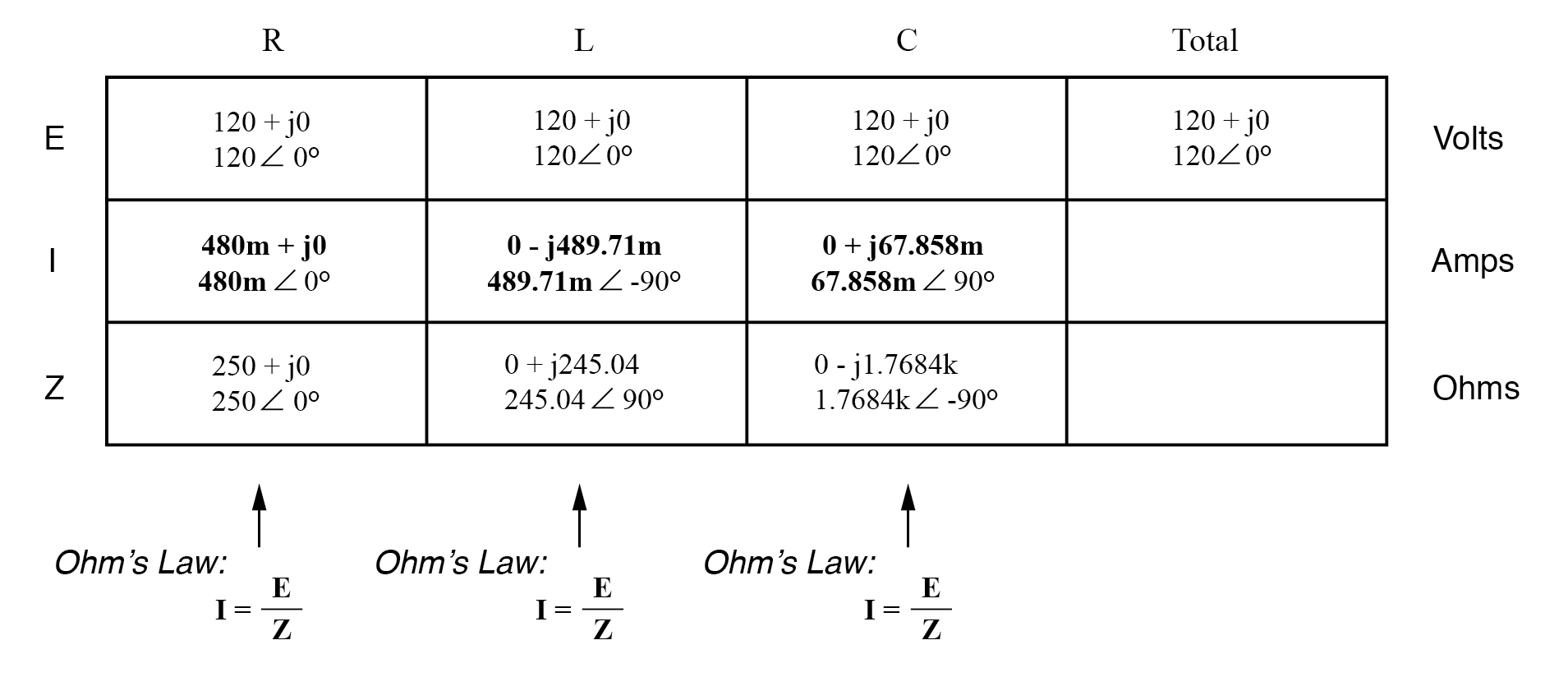	components values express as impedance image 3
 


Calculation of Total Current and Total Impedance

There are two strategies for calculating the total current and total
impedance. First, we could calculate total impedance from all the individual
impedances in parallel (ZTotal = 1/(1/ZR + 1/ZL + 1/ZC), and then calculate
total current by dividing source voltage by total impedance (I=E/Z).

However, working through the parallel impedance equation with complex
numbers is no easy task, with all the reciprocations (1/Z).

This is especially true if you’re unfortunate enough not to have a
calculator that handles complex numbers and are forced to do it all by hand
(reciprocate the individual impedances in polar form, then convert them all
to rectangular form for addition, then convert back to polar form for the
final inversion, then invert).

The second way to calculate total current and total impedance is to add up
all the branch currents to arrive at total current (total current in a
parallel circuit—AC or DC—is equal to the sum of the branch currents),
then use Ohm’s Law to determine total impedance from total voltage and
total current (Z=E/I).
	
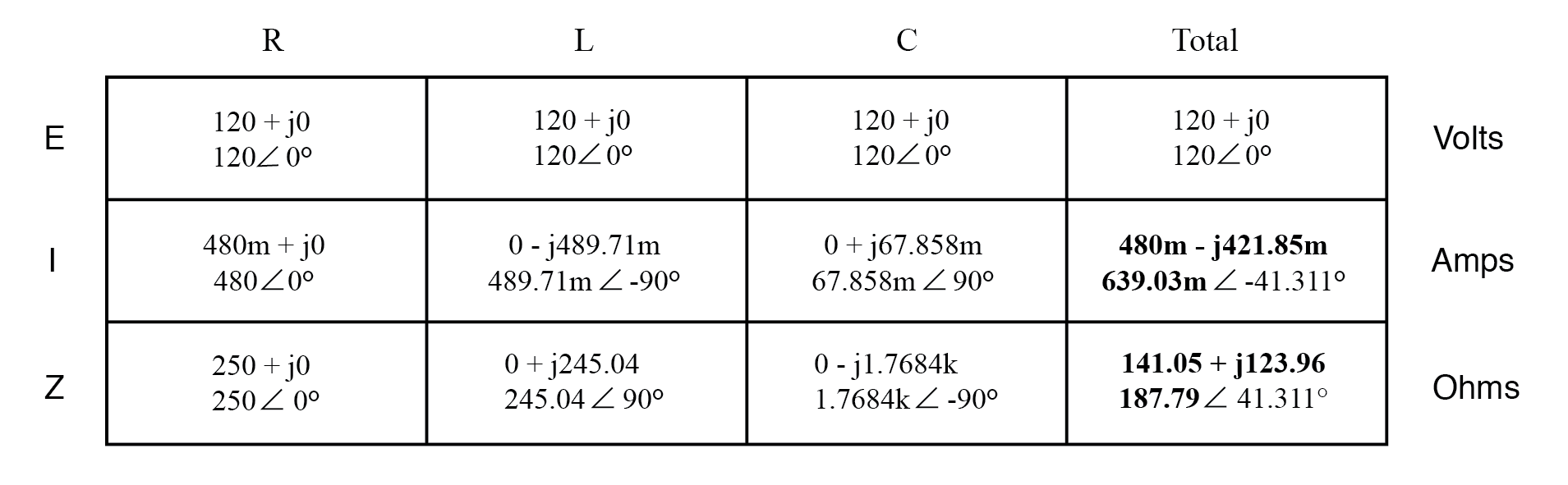	calculation of total current and total impedance

Either method, performed properly, will provide the correct answers. Let’s
try analyzing this circuit with SPICE and see what happens.
	
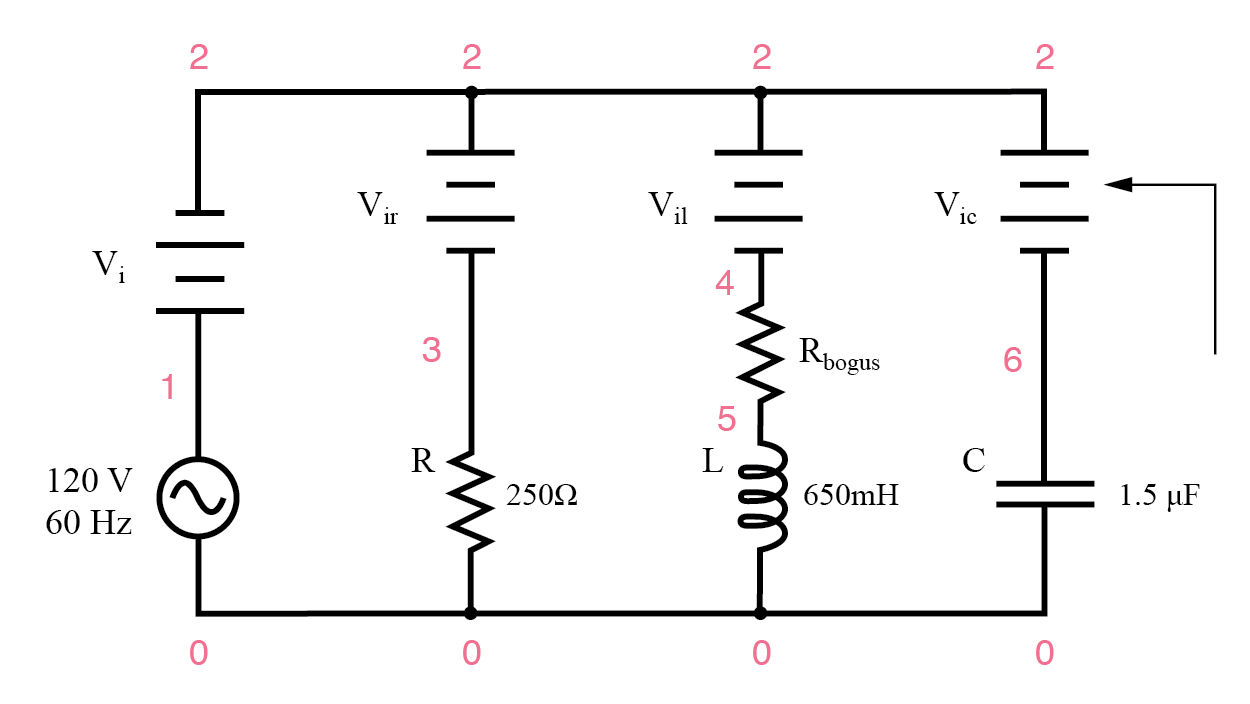	example parallel RLC spice circuit

Example parallel R, L, and C SPICE circuit. Battery symbols are “dummy”
voltage sources for SPICE to use as current measurement points. All are set
to 0 volts.

ac r-l-c circuit 
v1 1 0 ac 120 sin      
 
vi 1 2 ac 0     
vir 2 3 ac 0    
vil 2 4 ac 0    
rbogus 4 5 1e-12
vic 2 6 ac 0    
r1 3 0 250      
l1 5 0 650m     
c1 6 0 1.5u     
.ac lin 1 60 60 
.print ac i(vi) i(vir) i(vil) i(vic)   
 
.print ac ip(vi) ip(vir) ip(vil) ip(vic)
.end

freq          i(vi)       i(vir)      i(vil)      i(vic)      
6.000E+01     6.390E-01   4.800E-01   4.897E-01   6.786E-02

freq          ip(vi)      ip(vir)     ip(vil)     ip(vic)     
6.000E+01    -4.131E+01   0.000E+00  -9.000E+01   9.000E+01 

	
	interpreted spice results image 2

RELATED WORKSHEET: