If the waveform is a pure sine wave, the relationships between amplitudes
(peak-to-peak, peak) and RMS are fixed and known, as they are for any
continuous periodic wave. However, this is not true for an arbitrary
waveform, which may not be periodic or continuous. For a zero-mean sine
wave, the relationship between RMS and peak-to-peak amplitude is:
Peak-to-peak = 2 2 × RMS ≈ 2.8 × RMS . {\displaystyle =2{\sqrt
{2}}\times {\text{RMS}}\approx 2.8\times {\text{RMS}}.}
For other waveforms, the relationships are not the same as they are for
sine
waves. For example, for either a triangular or sawtooth wave
Peak-to-peak = 2 3 × RMS ≈ 3.5 × RMS . {\displaystyle =2{\sqrt
{3}}\times {\text{RMS}}\approx 3.5\times {\text{RMS}}.}
Waveform Variables and operators RMS
DC y = A 0 {\displaystyle y=A_{0}\,} A 0 {\displaystyle A_{0}\,}
Sine wave y = A 1 sin ( 2 π f t ) {\displaystyle y=A_{1}\sin(2\pi
ft)\,} A 1 2 {\displaystyle {\frac {A_{1}}{\sqrt {2}}}}
Square wave y = { A 1 frac ( f t ) < 0.5 − A 1 frac ( f t ) > 0.5 {\displaystyle
y={\begin{cases}A_{1}&\operatorname {frac} (ft)<0.5\\-A_{1}&\operatorname
{frac} (ft)>0.5\end{cases}}} A 1
{\displaystyle A_{1}\,}
DC-shifted square wave y = A 0 + { A 1 frac ( f t ) < 0.5 − A 1 frac ( f t ) > 0.5
{\displaystyle y=A_{0}+{\begin{cases}A_{1}&\operatorname {frac} (ft)
<0.5\\-A_{1}&\operatorname {frac}
(ft)>0.5\end{cases}}} A 0 2 + A 1 2 {\displaystyle {\sqrt
{A_{0}^{2}+A_{1}^{2}}}\,}
Modified sine wave y = { 0 frac ( f t ) < 0.25 A 1 0.25 < frac ( f
t ) < 0.5 0 0.5 < frac ( f t ) < 0.75 − A 1 frac ( f t ) > 0.75
{\displaystyle y={\begin{cases}0&\operatorname {frac} (ft)<
0.25\\A_{1}&0.25<operatorname {frac} (ft)<0.5\\0&0.5<operatorname {frac}
(ft)<0.75\\-A_{1}&\operatorname {frac} (ft)>0.75\end{cases}}} A 1 2
{\displaystyle {\frac {A_{1}}{\sqrt {2}}}}
Triangle wave y = | 2 A 1 frac ( f t ) − A 1 | {\displaystyle
y=\left|2A_{1}\operatorname {frac} (ft)-A_{1}\right|} A 1 3 {\displaystyle
A_{1} \over {\sqrt {3}}}
Sawtooth wave y = 2 A 1 frac ( f t ) − A 1 {\displaystyle
y=2A_{1}\operatorname {frac} (ft)-A_{1}\,} A 1 3 {\displaystyle A_{1}
\over
{\sqrt {3}}}
Pulse wave y = { A 1 frac ( f t ) < D 0 frac ( f t ) > D
{\displaystyle y={\begin{cases}A_{1}&\operatorname {frac} (
ft)<D\\0&\operatorname {frac} (ft)>D\end{cases}}} A 1 D {\displaystyle
A_{1}{\sqrt {D}}}
Phase-to-phase sine wave y = A 1 sin ( t ) − A 1 sin ( t − 2
π
3 ) {\displaystyle y=A_{1}\sin(t)-A_{1}\sin \left(t-{\frac {2\pi
}{3}}\right)\,} A 1 3 2 {\displaystyle A_{1}{\sqrt {\frac {3}{2}}}}
where:
y is displacement,
t is time,
f is frequency,
Ai is amplitude (peak value),
D is the duty cycle or the proportion of the time period (1/f) spent high,
frac(r) is the fractional part of r.
|
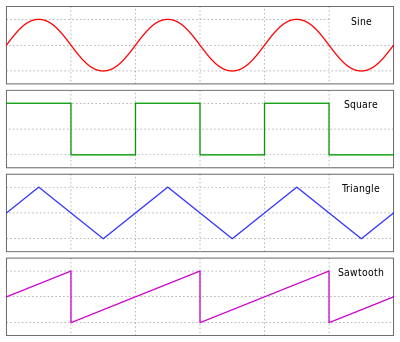 Sine, square, triangle, and sawtooth waveforms. In each, the centerline is
at 0, the positive peak is at y = A 1 {\displaystyle y=A_{1}} and the
negative peak is at y = − A 1 {\displaystyle y=-A_{1}}
Sine, square, triangle, and sawtooth waveforms. In each, the centerline is
at 0, the positive peak is at y = A 1 {\displaystyle y=A_{1}} and the
negative peak is at y = − A 1 {\displaystyle y=-A_{1}}
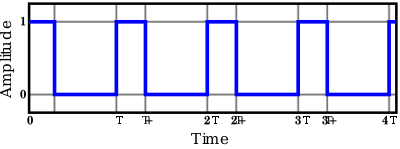 A rectangular pulse wave of duty cycle D, the ratio between the pulse
duration ( τ \tau ) and the period (T); illustrated here with a = 1.
A rectangular pulse wave of duty cycle D, the ratio between the pulse
duration ( τ \tau ) and the period (T); illustrated here with a = 1.
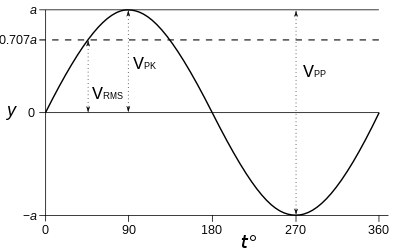 Graph of a sine wave's voltage vs. time (in degrees), showing RMS, peak
(PK), and peak-to-peak (PP) voltages.
Graph of a sine wave's voltage vs. time (in degrees), showing RMS, peak
(PK), and peak-to-peak (PP) voltages.
|
 Equation 1
This is well understood1 and there is no controversy here.
Now, let’s see how this compares with the value from an rms power calculation.
Figure 1 shows a graph of a 1 V rms sinusoid. The peak-to-peak value is 1 V
rms × 2 √2 = 2.828 V, swinging from +1.414 V to –1.414 V.2
Equation 1
This is well understood1 and there is no controversy here.
Now, let’s see how this compares with the value from an rms power calculation.
Figure 1 shows a graph of a 1 V rms sinusoid. The peak-to-peak value is 1 V
rms × 2 √2 = 2.828 V, swinging from +1.414 V to –1.414 V.2
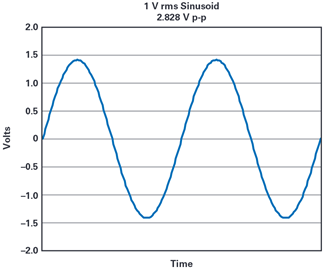 Figure 1. Graph of a 1 V rms sinusoid.
Figure 2 is a graph of the power dissipated by this 1 V rms sinusoid across
a 1 Ω resistor (P = V2/R) that shows:
Figure 1. Graph of a 1 V rms sinusoid.
Figure 2 is a graph of the power dissipated by this 1 V rms sinusoid across
a 1 Ω resistor (P = V2/R) that shows:
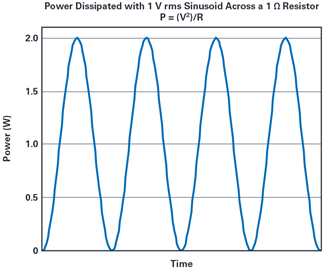 Figure 2. Graph of the power dissipated by a 1 V rms sinusoid across
a 1 Ω resistor.
Figure 2. Graph of the power dissipated by a 1 V rms sinusoid across
a 1 Ω resistor.
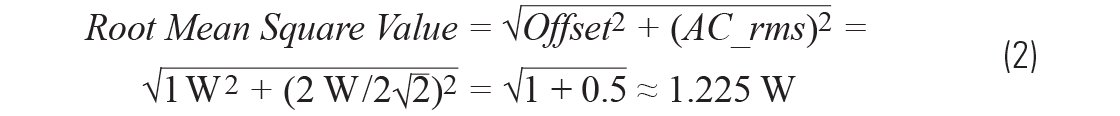 Equation 2
Equation 2
 Equation 3
Author
Doug Ito
Doug Ito is an applications engineer for the High Speed ADC team at Analog
Devices, Inc., San Diego, California. He earned a bachelor’s degree in
electrical engineering from San Diego State University. Doug is a member of
ADI’s EngineerZone® High Speed ADC Support Community.
=======================================================
Equation 3
Author
Doug Ito
Doug Ito is an applications engineer for the High Speed ADC team at Analog
Devices, Inc., San Diego, California. He earned a bachelor’s degree in
electrical engineering from San Diego State University. Doug is a member of
ADI’s EngineerZone® High Speed ADC Support Community.
=======================================================
 Sine, square, triangle, and sawtooth waveforms. In each, the centerline is
at 0, the positive peak is at y = A 1 {\displaystyle y=A_{1}} and the
negative peak is at y = − A 1 {\displaystyle y=-A_{1}}
Sine, square, triangle, and sawtooth waveforms. In each, the centerline is
at 0, the positive peak is at y = A 1 {\displaystyle y=A_{1}} and the
negative peak is at y = − A 1 {\displaystyle y=-A_{1}}
 A rectangular pulse wave of duty cycle D, the ratio between the pulse
duration ( τ \tau ) and the period (T); illustrated here with a = 1.
A rectangular pulse wave of duty cycle D, the ratio between the pulse
duration ( τ \tau ) and the period (T); illustrated here with a = 1.
 Graph of a sine wave's voltage vs. time (in degrees), showing RMS, peak
(PK), and peak-to-peak (PP) voltages.
Graph of a sine wave's voltage vs. time (in degrees), showing RMS, peak
(PK), and peak-to-peak (PP) voltages.
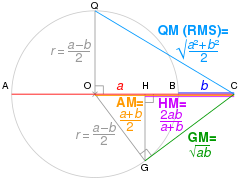 Geometric proof without words that max (a,b) > root mean square (RMS) or
quadratic mean (QM) > arithmetic mean (AM) > geometric mean (GM) > harmonic
mean (HM) > min (a,b) of two distinct positive numbers a and b [note 1]
Geometric proof without words that max (a,b) > root mean square (RMS) or
quadratic mean (QM) > arithmetic mean (AM) > geometric mean (GM) > harmonic
mean (HM) > min (a,b) of two distinct positive numbers a and b [note 1]