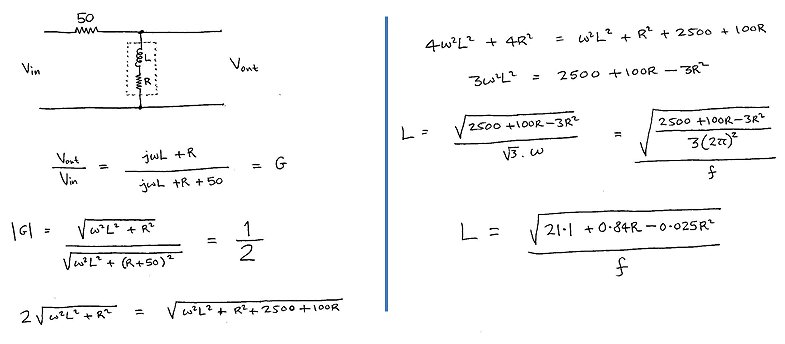Simple Method to Measure Inductance
From: https://www.dos4ever.com/inductor/inductor.html
Simple Method to Measure Unknown Inductors
A simple and quick way to measure the inductance of an unknown power inductor
(provided you have a function generator and oscilloscope).
Ronald Dekker
|
|
Contents:
|
 |
1. Introduction
Whenever I can I always salvage (power) inductors from old PCBs and switched
mode power supplies. A good assortment of different value inductors always
comes in handy during experiments, especially with boost converters and the
like. Now, I am sure that there must be a system by which manufacturers of
these inductors mark them with the inductance value, but so far I have not
been able to discover it. Some inductors have some numbers printed on them,
while others are marked with colored dots which are a disaster anyway
because I am color blind. To quickly sort out the inductance value of these
inductors I use a simple method which I am sure will interest other inductor
ignorami. The tools you need are a 0-100 kHz function generator WITH 50 OHM
OUTPUT, and an oscilloscope. to top of page back to homepage
2. The Method Step-by-Step
Since most people will be more interested in the method rather than in the
theory behind it, let┐s start with a step-by-step description:
- Connect the 50 ohm output of the function generator to the oscilloscope,
and select a sine-wave signal.
- Adjust the frequency of the generator to approximately 20 kHz.
- Adjust the output voltage of the generator to 1 V peak-peak.
- Connect the unknown inductor parallel to the oscilloscope (Fig. 2.1).
Doing so will decrease the amplitude of the signal.
- Now adjust only the frequency of the generator in such a way that the
amplitude on the oscilloscope is exactly half the original value (0.5V pp).
The way I execute steps 3 to 5 is as follows: In step 3 I first set the
vertical sensitivity of the scope to 0.2 V/div. Then I adjust the amplitude
of the signal generator so that the sine wave exactly fits between the 25%
and 75% markings on the screen (Fig. 2.1A). The amplitude is now exactly 1V.
Next I connect the inductor (step 4), and increase the vertical sensitivity
to 0.1 V/div. In step 5 I now adjust the frequency so that the sine wave
again exactly fits in between the 25% and 75% markings (Fig. 2.1B). The
amplitude of the sine wave is now 0.5 V.
- Finally, read out the frequency, and calculate the inductance from
L=4.57/f. With L in Henry and f in Hz. You may also prefer L=4570/f with L
in uH and f in kHz.
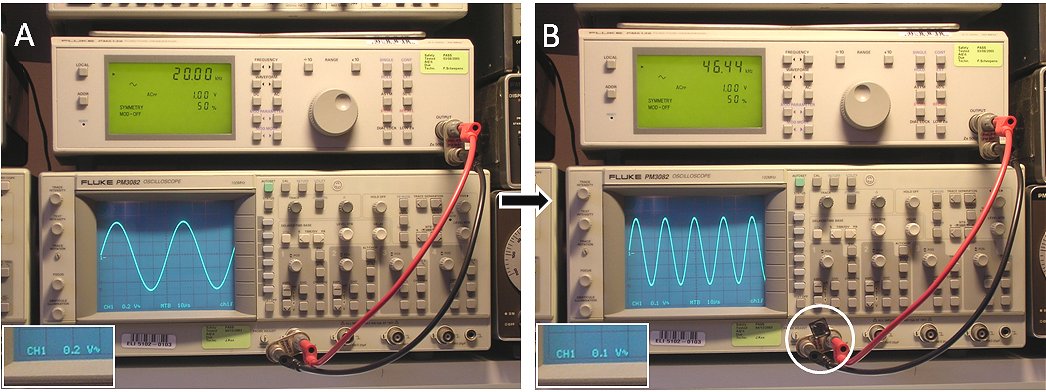 Figure 2.1 Measuring unknown inductors.
Figure 2.1 Measuring unknown inductors.
to top of page back to homepage
3. How it Works & some Theory
The inductor, in combination with the internal series resistance in the
generator form a voltage divider circuit (Fig. 3.1). Without the inductor
connected, the voltage drop over the 50 ohm resistor is negligible and the
oscilloscope displays the ┐internal┐ voltage of the generator. With the
inductor connected, the current through the inductor will cause a voltage
drop over the 50 ohm resistor causing the amplitude of the signal on the
screen of the scope to drop. The current through the inductor is a function
of both the frequency as well as the inductance. For a DC signals (0 Hz) the
inductor represents a short circuit. For very high frequencies to current
through the inductor is negligible. Furthermore, for a given frequency, the
higher the inductance, the lower the current.
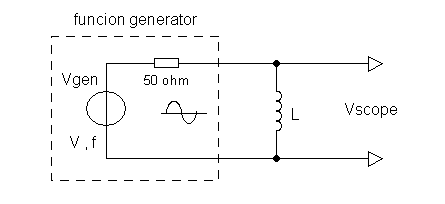 Figure 3.1 The ┐circuit diagram┐
The exact ratio between the internal generator voltage and the voltage measured
by the scope can be calculated with a bit of straightforward network theory:
Figure 3.1 The ┐circuit diagram┐
The exact ratio between the internal generator voltage and the voltage measured
by the scope can be calculated with a bit of straightforward network theory:
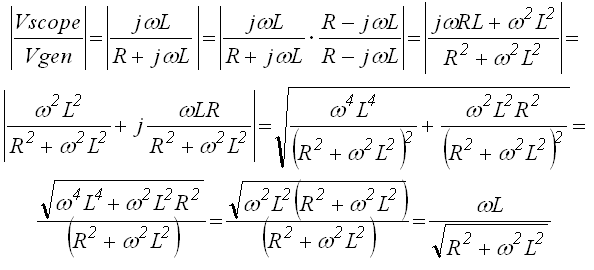 In this formula L represent the inductance, R the resistance (50 ohm), and
omega the radial frequency ( = 2*pi*f with f in Hz).
The question now is for what frequency (Vscope/Vgen) = 0.5:
In this formula L represent the inductance, R the resistance (50 ohm), and
omega the radial frequency ( = 2*pi*f with f in Hz).
The question now is for what frequency (Vscope/Vgen) = 0.5:
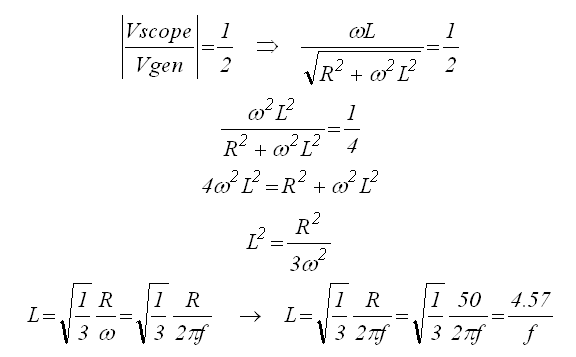 So finally:
In which L is the inductance in Henry, and f the frequency in Hz.
This method only works well for inductors with a low series resistance,
and an inductance in the range of say 10 to several hundreds of uH.
So finally:
In which L is the inductance in Henry, and f the frequency in Hz.
This method only works well for inductors with a low series resistance,
and an inductance in the range of say 10 to several hundreds of uH.
4. Including Series Resistance.
The nice thing about a website is that people from time to time make very
useful contributions. Karen Orton (UK) improved the method proposed above
for inductors which have a significant resistance. Simply DC measure the
resistance first and use it in the formula below. Otherwise the procedure is
exactly as described above.
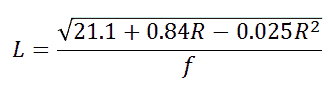 Here is the math in Karen┐s own hand:
Here is the math in Karen┐s own hand:
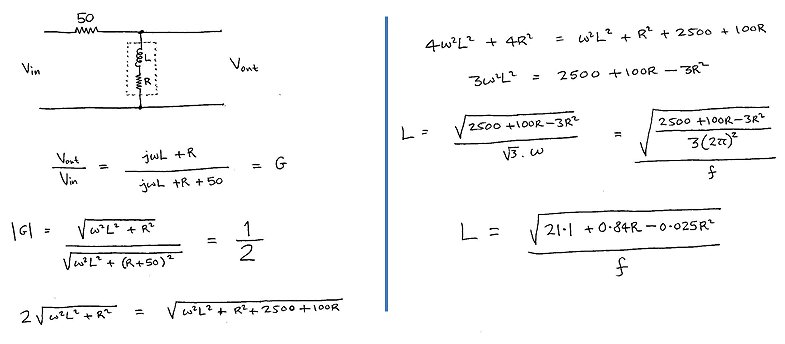


 Figure 2.1 Measuring unknown inductors.
Figure 2.1 Measuring unknown inductors.
 Figure 3.1 The ┐circuit diagram┐
The exact ratio between the internal generator voltage and the voltage measured
by the scope can be calculated with a bit of straightforward network theory:
Figure 3.1 The ┐circuit diagram┐
The exact ratio between the internal generator voltage and the voltage measured
by the scope can be calculated with a bit of straightforward network theory:
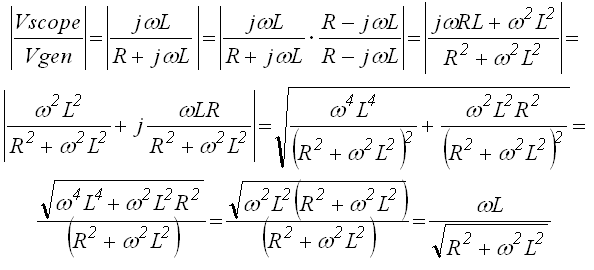 In this formula L represent the inductance, R the resistance (50 ohm), and
omega the radial frequency ( = 2*pi*f with f in Hz).
The question now is for what frequency (Vscope/Vgen) = 0.5:
In this formula L represent the inductance, R the resistance (50 ohm), and
omega the radial frequency ( = 2*pi*f with f in Hz).
The question now is for what frequency (Vscope/Vgen) = 0.5:
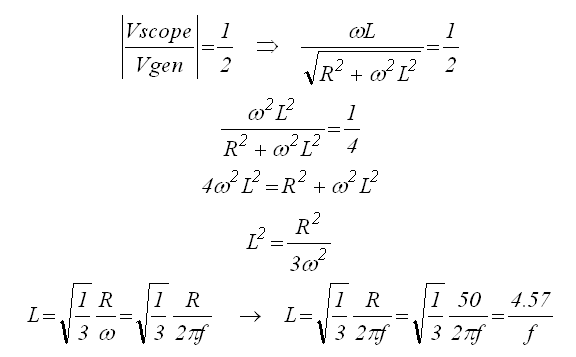 So finally:
In which L is the inductance in Henry, and f the frequency in Hz.
This method only works well for inductors with a low series resistance,
and an inductance in the range of say 10 to several hundreds of uH.
So finally:
In which L is the inductance in Henry, and f the frequency in Hz.
This method only works well for inductors with a low series resistance,
and an inductance in the range of say 10 to several hundreds of uH.
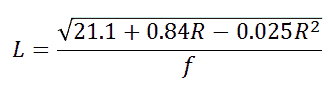 Here is the math in Karen┐s own hand:
Here is the math in Karen┐s own hand: